Machine Learning With Tidyverse
Suppose in the street if someone asks me what is meant by Machine Learning, my quick, top of my head answer will be - its an art of gathering and extracting valuable information from the past data using statistical tools to come up with a model or understanding to predict the future. It could be something like studying data on old market trend to come up with a way to predict the future trend. Imagine what better will we be, if we could predict the future.
In this post, however, we are using a dataset and generate 2 sets of model. We evaluate the performances of both the models and decide which one works best for the prediction. We are using a dataset called gapminder and use tidyverse to wrangle our data. We will built 2 models namely Linear Regression and Random Forest. Let’s load some libraries and start our process.
my_data<-gapminder %>%
select(-continent)
my_data %>%
count(country, sort=TRUE)## # A tibble: 142 x 2
## country n
## <fct> <int>
## 1 Afghanistan 12
## 2 Albania 12
## 3 Algeria 12
## 4 Angola 12
## 5 Argentina 12
## 6 Australia 12
## 7 Austria 12
## 8 Bahrain 12
## 9 Bangladesh 12
## 10 Belgium 12
## # ... with 132 more rowshead(my_data)## # A tibble: 6 x 5
## country year lifeExp pop gdpPercap
## <fct> <int> <dbl> <int> <dbl>
## 1 Afghanistan 1952 28.8 8425333 779.
## 2 Afghanistan 1957 30.3 9240934 821.
## 3 Afghanistan 1962 32.0 10267083 853.
## 4 Afghanistan 1967 34.0 11537966 836.
## 5 Afghanistan 1972 36.1 13079460 740.
## 6 Afghanistan 1977 38.4 14880372 786.gapminder is a dataset of 142 countries with details like life expectancy, population and gdp-per-capita on yearly basis. We call these factors or variables. Some factors are independent while some depend on others. In machine learning field, we generally study the relation, if there exists, between these two factors. In our case we will be trying to study the relationship between life expectancy with other factors.
As usual lets tidy up our data for easy analysis.
my_data_nested<- my_data %>%
group_by(country) %>%
nest()
my_data_nested## # A tibble: 142 x 2
## country data
## <fct> <list>
## 1 Afghanistan <tibble [12 x 4]>
## 2 Albania <tibble [12 x 4]>
## 3 Algeria <tibble [12 x 4]>
## 4 Angola <tibble [12 x 4]>
## 5 Argentina <tibble [12 x 4]>
## 6 Australia <tibble [12 x 4]>
## 7 Austria <tibble [12 x 4]>
## 8 Bahrain <tibble [12 x 4]>
## 9 Bangladesh <tibble [12 x 4]>
## 10 Belgium <tibble [12 x 4]>
## # ... with 132 more rowsI grouped data by country and made a list column. I have defined more about list column in my previous posts. For simplicity lets imagine its like entire work sheet stored into a tiny cell. First I will show a simple model by using just 2 factors.
Linear Regression
Linear Regression is one of the most basic and power statistical models. The equation looks like
Y = a + bX
Here, a is y-intercept and b is slope. These are two unknown quantities in my equation (model). I have to find the best values for these quantites which minimizes error on prediction. I’m mostly interested in value b. It shows how in average the trend is increasing or decreasing in given year.
my_data_tidied<-my_data_nested %>%
mutate(model = map(data, ~lm(lifeExp~year, data = .)),
tidied = map(model, tidy)) %>%
unnest(tidied)
my_data_tidied## # A tibble: 284 x 6
## country term estimate std.error statistic p.value
## <fct> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Afghanistan (Intercept) -508. 40.5 -12.5 1.93e- 7
## 2 Afghanistan year 0.275 0.0205 13.5 9.84e- 8
## 3 Albania (Intercept) -594. 65.7 -9.05 3.94e- 6
## 4 Albania year 0.335 0.0332 10.1 1.46e- 6
## 5 Algeria (Intercept) -1068. 43.8 -24.4 3.07e-10
## 6 Algeria year 0.569 0.0221 25.7 1.81e-10
## 7 Angola (Intercept) -377. 46.6 -8.08 1.08e- 5
## 8 Angola year 0.209 0.0235 8.90 4.59e- 6
## 9 Argentina (Intercept) -390. 9.68 -40.3 2.14e-12
## 10 Argentina year 0.232 0.00489 47.4 4.22e-13
## # ... with 274 more rowsWith the help of nested lists, I can generate multiple models for each country. If you look into our first result, Afganistan, the year estimate is 0.275. It shows on average life expectancy of Afganistan increases by 0.275.
Moverover, I can find out how my model behaved with each country, meaning how each model fit my data. One way to tell this is by knowing R.squared (R²)
R² is always between 0 and 1. The higher the R², the better our model in explaining. In other terms it can be seen as out of total % of variance, how much % of varince is successfully exlained by the model.
my_data_glanced<-my_data_nested %>%
mutate(model = map(data, ~lm(lifeExp~year, data = .)),
glanced = map(model, glance)) %>%
unnest(glanced)
my_data_glanced## # A tibble: 142 x 14
## country data model r.squared adj.r.squared sigma statistic p.value
## <fct> <lis> <lis> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Afghan~ <tib~ <S3:~ 0.948 0.942 1.22 181. 9.84e- 8
## 2 Albania <tib~ <S3:~ 0.911 0.902 1.98 102. 1.46e- 6
## 3 Algeria <tib~ <S3:~ 0.985 0.984 1.32 662. 1.81e-10
## 4 Angola <tib~ <S3:~ 0.888 0.877 1.41 79.1 4.59e- 6
## 5 Argent~ <tib~ <S3:~ 0.996 0.995 0.292 2246. 4.22e-13
## 6 Austra~ <tib~ <S3:~ 0.980 0.978 0.621 481. 8.67e-10
## 7 Austria <tib~ <S3:~ 0.992 0.991 0.407 1261. 7.44e-12
## 8 Bahrain <tib~ <S3:~ 0.967 0.963 1.64 291. 1.02e- 8
## 9 Bangla~ <tib~ <S3:~ 0.989 0.988 0.977 930. 3.37e-11
## 10 Belgium <tib~ <S3:~ 0.995 0.994 0.293 1822. 1.20e-12
## # ... with 132 more rows, and 6 more variables: df <int>, logLik <dbl>,
## # AIC <dbl>, BIC <dbl>, deviance <dbl>, df.residual <int>I used similar approach as before but this time we used glance function from broom package. Here you can see r.squared values of each country. Lets find out top best and worst r.squared.
Best R²
best_one<-my_data_glanced %>%
top_n(1, r.squared)
best_one## # A tibble: 1 x 14
## country data model r.squared adj.r.squared sigma statistic p.value
## <fct> <lis> <lis> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Brazil <tib~ <S3:~ 0.998 0.998 0.326 5111. 6.99e-15
## # ... with 6 more variables: df <int>, logLik <dbl>, AIC <dbl>, BIC <dbl>,
## # deviance <dbl>, df.residual <int>Worst R²
worst_one<- my_data_glanced %>%
top_n(1, -r.squared)
worst_one## # A tibble: 1 x 14
## country data model r.squared adj.r.squared sigma statistic p.value df
## <fct> <lis> <lis> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
## 1 Rwanda <tib~ <S3:~ 0.0172 -0.0811 6.56 0.175 0.685 2
## # ... with 5 more variables: logLik <dbl>, AIC <dbl>, BIC <dbl>,
## # deviance <dbl>, df.residual <int>We can see Brazil has the best fit while Rwanda has the worst one. I can show using augment function of `broom’ package.
my_data_augmented<-my_data_nested %>%
mutate(model = map(data, ~lm(lifeExp~year, data = .)),
augmented = map(model, augment)) %>%
unnest(augmented)
my_data_augmented## # A tibble: 1,704 x 10
## country lifeExp year .fitted .se.fit .resid .hat .sigma .cooksd
## <fct> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Afghan~ 28.8 1952 29.9 0.664 -1.11 0.295 1.21 2.43e-1
## 2 Afghan~ 30.3 1957 31.3 0.580 -0.952 0.225 1.24 1.13e-1
## 3 Afghan~ 32.0 1962 32.7 0.503 -0.664 0.169 1.27 3.60e-2
## 4 Afghan~ 34.0 1967 34.0 0.436 -0.0172 0.127 1.29 1.65e-5
## 5 Afghan~ 36.1 1972 35.4 0.385 0.674 0.0991 1.27 1.85e-2
## 6 Afghan~ 38.4 1977 36.8 0.357 1.65 0.0851 1.15 9.23e-2
## 7 Afghan~ 39.9 1982 38.2 0.357 1.69 0.0851 1.15 9.67e-2
## 8 Afghan~ 40.8 1987 39.5 0.385 1.28 0.0991 1.21 6.67e-2
## 9 Afghan~ 41.7 1992 40.9 0.436 0.754 0.127 1.26 3.17e-2
## 10 Afghan~ 41.8 1997 42.3 0.503 -0.534 0.169 1.27 2.33e-2
## # ... with 1,694 more rows, and 1 more variable: .std.resid <dbl>I can visually see how model fitted the data for these two countries.
my_data_augmented %>%
filter(country %in% c("Brazil", "Rwanda")) %>%
group_by(country) %>%
ggplot(aes(year,lifeExp))+
geom_point(size = 1.5)+
geom_line(aes(y = .fitted, color = "Red"), show.legend = FALSE)+
facet_wrap(~country,nrow = 2)+
labs(title = "How model fitted the data")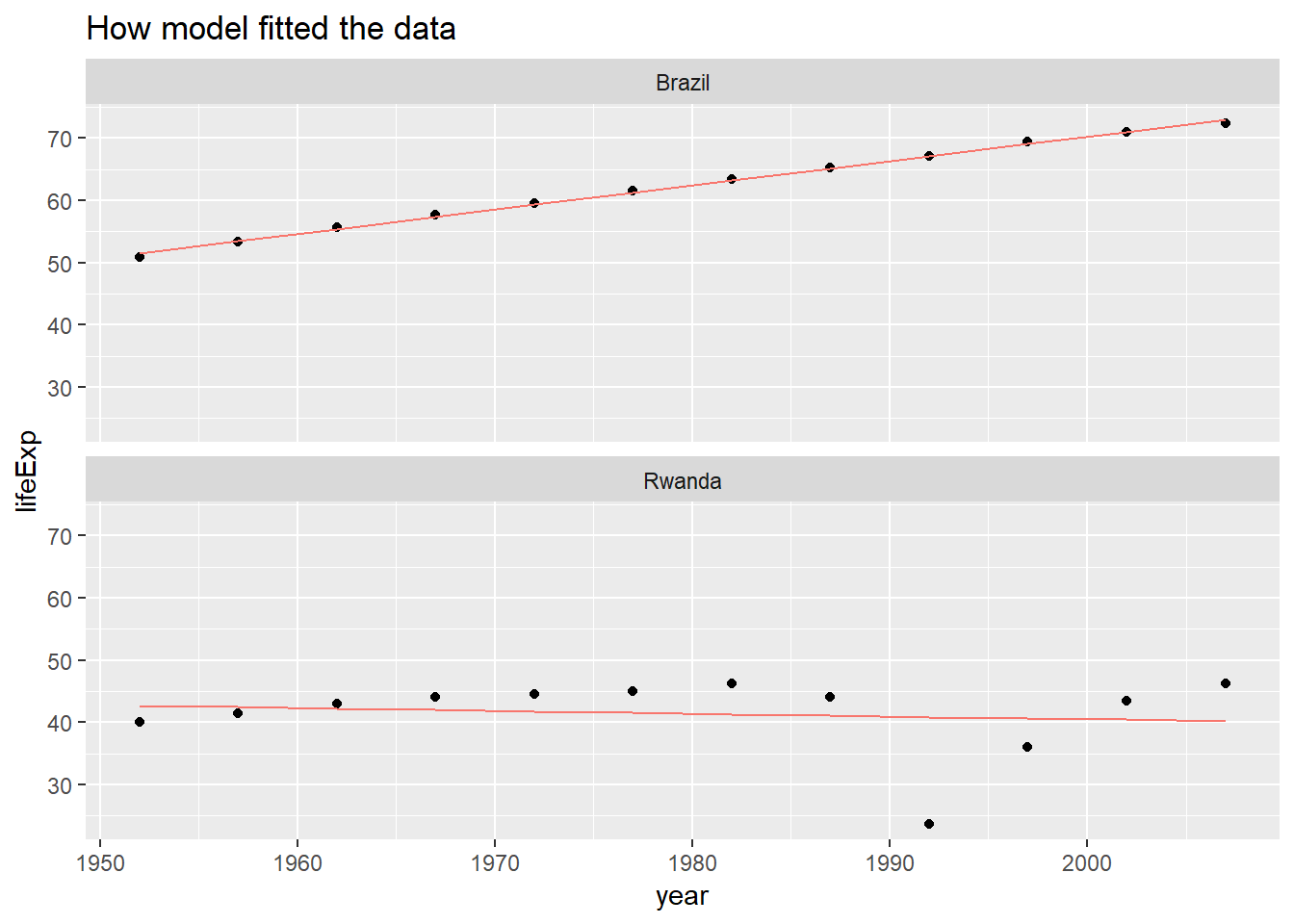
As you can see, the red line represts my model, while the dots are my data points. In the case of Brazil, we can see how the line went perfectly inside each points while on the other we see how the line deviated from the points. One important thing to note is we shouldn’t think the model which we see for Brazil is the ideal one. In fact, even it has high R², this model can perform bad on prediction due to Overfitting. Overfitting occurs when our model learns a lot such that it stats to generalise everything. We should avoid this.
One way to avoid this is by a proces called Cross Validation. In this we divide our dataset into train, validate and test sets, instead of training our whole dataset.
Now lets switch some gears. Until now I have just shown a simple model with just two variables and there is no any data splits. From now I’m going to follow above steps-
Split data in multiple sets. First training and test test. We again split our
training setinto 3 folds. In each fold, there will be different validation set.Generate 2 types of Models
Evaluate the best model by looking into its perfomance
Use that best model to predict on the
test set.
Split data
gap_split <-initial_split(my_data, prop = 0.75)
training_data <- training(gap_split)
testing_data <- testing(gap_split)
cv_splits <- vfold_cv(training_data, v = 3)
cv_splits## # 3-fold cross-validation
## # A tibble: 3 x 2
## splits id
## <list> <chr>
## 1 <split [852/426]> Fold1
## 2 <split [852/426]> Fold2
## 3 <split [852/426]> Fold3cv_dataset <- cv_splits %>%
mutate(train_set = map(splits, ~training(.)),
validate_set = map(splits, ~testing(.)))
cv_dataset## # 3-fold cross-validation
## # A tibble: 3 x 4
## splits id train_set validate_set
## * <list> <chr> <list> <list>
## 1 <split [852/426]> Fold1 <tibble [852 x 5]> <tibble [426 x 5]>
## 2 <split [852/426]> Fold2 <tibble [852 x 5]> <tibble [426 x 5]>
## 3 <split [852/426]> Fold3 <tibble [852 x 5]> <tibble [426 x 5]>Here, I have first split my gapminder dataset into training and testing set. The testing set will only be used after the best model is found. Again, I split the training set into 3 folds.
Now lets build 2 models
Multiple Linear Regression
mul_reg_model<-cv_dataset %>%
mutate(model_mulreg = map(train_set, ~lm(lifeExp ~ ., data = .)))
mul_reg_model## # 3-fold cross-validation
## # A tibble: 3 x 5
## splits id train_set validate_set model_mulreg
## * <list> <chr> <list> <list> <list>
## 1 <split [852/426]> Fold1 <tibble [852 x 5]> <tibble [426 x 5~ <S3: lm>
## 2 <split [852/426]> Fold2 <tibble [852 x 5]> <tibble [426 x 5~ <S3: lm>
## 3 <split [852/426]> Fold3 <tibble [852 x 5]> <tibble [426 x 5~ <S3: lm>Random Forest
ran_for_model<-cv_dataset %>%
mutate(model_ranfor = map(train_set, ~ranger(lifeExp ~., data = ., seed = 42)))
ran_for_model## # 3-fold cross-validation
## # A tibble: 3 x 5
## splits id train_set validate_set model_ranfor
## * <list> <chr> <list> <list> <list>
## 1 <split [852/426]> Fold1 <tibble [852 x 5]> <tibble [426 x 5~ <S3: ranger>
## 2 <split [852/426]> Fold2 <tibble [852 x 5]> <tibble [426 x 5~ <S3: ranger>
## 3 <split [852/426]> Fold3 <tibble [852 x 5]> <tibble [426 x 5~ <S3: ranger>I have built 2 models. As you can see in these models I have used all the factors. I haven’t tweaked our models by using any hyper parameters. You can view them as nots and bolts, which you can play round to take out maximum output from any model. I used the basic ones to make it simpler for you to understand.
Model Evaluation
First lets extract lifeExp values from our validation set and store into actual_score, which I will compare with my prediction score to find out how good my model did on predicting. Second I will use my models into corresponding validate sets to get predicted_score.
mul_reg_model<-mul_reg_model %>%
mutate(actual_score = map(validate_set, ~.$lifeExp),
predicted_score = map2(model_mulreg,validate_set, ~predict(.x,.y)))
mul_reg_model## # 3-fold cross-validation
## # A tibble: 3 x 7
## splits id train_set validate_set model_mulreg actual_score
## * <list> <chr> <list> <list> <list> <list>
## 1 <spli~ Fold1 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## 2 <spli~ Fold2 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## 3 <spli~ Fold3 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## # ... with 1 more variable: predicted_score <list>ran_for_model<-ran_for_model %>%
mutate(actual_score = map(validate_set, ~.$lifeExp),
predicted_score = map2(model_ranfor, validate_set, ~predict(.x,.y)$predictions))
ran_for_model## # 3-fold cross-validation
## # A tibble: 3 x 7
## splits id train_set validate_set model_ranfor actual_score
## * <list> <chr> <list> <list> <list> <list>
## 1 <spli~ Fold1 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## 2 <spli~ Fold2 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## 3 <spli~ Fold3 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## # ... with 1 more variable: predicted_score <list>For model evaluation I will be using Mean Absolute Error (MAE) metrics.
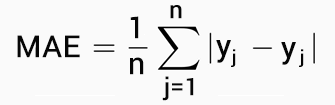
mul_reg_model<-mul_reg_model %>%
mutate(mae = map2_dbl(actual_score,predicted_score,~mae(.x,.y)))
mul_reg_model## # 3-fold cross-validation
## # A tibble: 3 x 8
## splits id train_set validate_set model_mulreg actual_score
## * <list> <chr> <list> <list> <list> <list>
## 1 <spli~ Fold1 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## 2 <spli~ Fold2 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## 3 <spli~ Fold3 <tibble ~ <tibble [42~ <S3: lm> <dbl [426]>
## # ... with 2 more variables: predicted_score <list>, mae <dbl>ran_for_model<-ran_for_model %>%
mutate(mae = map2_dbl(actual_score,predicted_score,~mae(.x,.y)))
ran_for_model## # 3-fold cross-validation
## # A tibble: 3 x 8
## splits id train_set validate_set model_ranfor actual_score
## * <list> <chr> <list> <list> <list> <list>
## 1 <spli~ Fold1 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## 2 <spli~ Fold2 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## 3 <spli~ Fold3 <tibble ~ <tibble [42~ <S3: ranger> <dbl [426]>
## # ... with 2 more variables: predicted_score <list>, mae <dbl>To find out which model is best out of 2, I need to see the mean of MAE of both.
mean(mul_reg_model$mae)## [1] 2.898502mean(ran_for_model$mae)## [1] 3.961781Here, it seems MAE of my Multiple Linear Regression is lower and I can call this as best model of 2. Now lets use this model into my final test set.
Predict on test set
best_model <- lm(lifeExp~., data = training_data)
actual_test_score <-testing_data$lifeExp
predicted_test_score <- predict(best_model, testing_data)
testing_mae <- mae(actual_test_score, predicted_test_score)
testing_mae## [1] 2.616323This value is called Model Test Performance Value.
Conclusion
The method defined above to do analysis is one of the classic ways of doing Machine Learning. There are many aspects which I have overlooked to simplify the process. For example I used basic models with no hyper parameter tuning. A lot can be achieved by employing this method, which I didn’t. There are sophisticated ways of doing Cross Validation like k-fold cross validation, which can further help to create better model. Similarly, I have heavily over-estimated other statistical values like adusted r.square, p-values.
